Napier's abacus 1.0

for Huawei Honor 5X

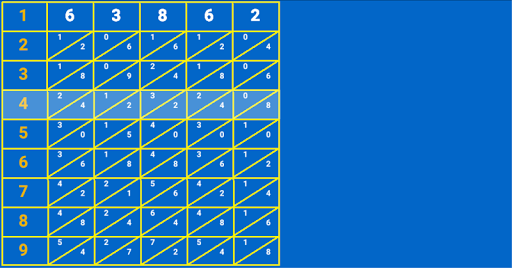
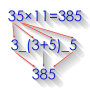
This abacus was created by John Napier of Merchiston in 1617 for calculation of products and quotients of numbers. The method was based on Arab mathematics and the lattice multiplication. Using the multiplication tables embedded in the rods, multiplication can be reduced to addition operations and division to subtractions. More advanced use of the rods can even extract square roots. The abacus consists of a board with a rim; the App places Napier's rods in the rim to conduct multiplication or division. The board's left edge is divided into 9 squares, holding the numbers 1 to 9. A rod's surface comprises 9 squares, and each square, except for the top one, comprises two halves divided by a diagonal line. The first square of each rod holds a single digit, and the other squares hold this number's double, triple, quadruple, quintuple, and so on until the last square contains nine times the number in the top square. The digits of each product are written one to each side of the diagonal; numbers less than 10 occupy the lower triangle, with a zero in the top half.
Napier's abacus concept can be adopted as a technique to teach multiplication for students in the fifth and sixth grade that makes mathematics interesting. Furthermore, this technique can also be used for students at higher levels. Conventional method of teaching is not enough in teaching learning process in mathematics, moreover in elementary school.

Input the number and build Napier's abacus; touch the numbers on the left to highlight the relative row.

Learn more on http://en.wikipedia.org/wiki/Napier's_bones